map 的扩容过程是怎样的

使用哈希表的目的就是要快速查找到目标 key，然而，随着向 map 中添加的 key 越来越多，key 发生碰撞的概率也越来越大。bucket 中的 8 个 cell 会被逐渐塞满，查找、插入、删除 key 的效率也会越来越低。最理想的情况是一个 bucket 只装一个 key，这样，就能达到 O(1) 的效率，但这样空间消耗太大，用空间换时间的代价太高。

Go 语言采用一个 bucket 里装载 8 个 key，定位到某个 bucket 后，还需要再定位到具体的 key，这实际上又用了时间换空间。

当然，这样做，要有一个度，不然所有的 key 都落在了同一个 bucket 里，直接退化成了链表，各种操作的效率直接降为 O(n)，是不行的。

因此，需要有一个指标来衡量前面描述的情况，这就是装载因子。Go 源码里这样定义 装载因子：

loadFactor := count / (2^B)

count 就是 map 的元素个数，2^B 表示 bucket 数量。

再来说触发 map 扩容的时机：在向 map 插入新 key 的时候，会进行条件检测，符合下面这 2 个条件，就会触发扩容：

1. 装载因子超过阈值，源码里定义的阈值是 6.5。

2. overflow 的 bucket 数量过多：当 B 小于 15，也就是 bucket 总数 2^B 小于 2^15 时，如果 overflow 的 bucket 数量超过 2^B；当 B >= 15，也就是 bucket 总数 2^B 大于等于 2^15，如果 overflow 的 bucket 数量超过 2^15。

通过汇编语言可以找到赋值操作对应源码中的函数是 mapassign，对应扩容条件的源码如下：

// src/runtime/hashmap.go/mapassign

// 触发扩容时机
if !h.growing() && (overLoadFactor(int64(h.count), h.B) || tooManyOverflowBuckets(h.noverflow, h.B)) {
        hashGrow(t, h)
    }

// 装载因子超过 6.5
func overLoadFactor(count int64, B uint8) bool {
    return count >= bucketCnt && float32(count) >= loadFactor*float32((uint64(1)<<B))
}

// overflow buckets 太多
func tooManyOverflowBuckets(noverflow uint16, B uint8) bool {
    if B < 16 {
        return noverflow >= uint16(1)<<B
    }
    return noverflow >= 1<<15
}

解释一下：

第 1 点：我们知道，每个 bucket 有 8 个空位，在没有溢出，且所有的桶都装满了的情况下，装载因子算出来的结果是 8。因此当装载因子超过 6.5 时，表明很多 bucket 都快要装满了，查找效率和插入效率都变低了。在这个时候进行扩容是有必要的。

第 2 点：是对第 1 点的补充。就是说在装载因子比较小的情况下，这时候 map 的查找和插入效率也很低，而第 1 点识别不出来这种情况。表面现象就是计算装载因子的分子比较小，即 map 里元素总数少，但是 bucket 数量多（真实分配的 bucket 数量多，包括大量的 overflow bucket）。

不难想像造成这种情况的原因：不停地插入、删除元素。先插入很多元素，导致创建了很多 bucket，但是装载因子达不到第 1 点的临界值，未触发扩容来缓解这种情况。之后，删除元素降低元素总数量，再插入很多元素，导致创建很多的 overflow bucket，但就是不会触犯第 1 点的规定，你能拿我怎么办？overflow bucket 数量太多，导致 key 会很分散，查找插入效率低得吓人，因此出台第 2 点规定。这就像是一座空城，房子很多，但是住户很少，都分散了，找起人来很困难。

对于命中条件 1，2 的限制，都会发生扩容。但是扩容的策略并不相同，毕竟两种条件应对的场景不同。

对于条件 1，元素太多，而 bucket 数量太少，很简单：将 B 加 1，bucket 最大数量（2^B）直接变成原来 bucket 数量的 2 倍。于是，就有新老 bucket 了。注意，这时候元素都在老 bucket 里，还没迁移到新的 bucket 来。而且，新 bucket 只是最大数量变为原来最大数量（2^B）的 2 倍（2^B * 2）。

对于条件 2，其实元素没那么多，但是 overflow bucket 数特别多，说明很多 bucket 都没装满。解决办法就是开辟一个新 bucket 空间，将老 bucket 中的元素移动到新 bucket，使得同一个 bucket 中的 key 排列地更紧密。这样，原来，在 overflow bucket 中的 key 可以移动到 bucket 中来。结果是节省空间，提高 bucket 利用率，map 的查找和插入效率自然就会提升。

对于条件 2 的解决方案，曹大的博客里还提出了一个极端的情况：如果插入 map 的 key 哈希都一样，就会落到同一个 bucket 里，超过 8 个就会产生 overflow bucket，结果也会造成 overflow bucket 数过多。移动元素其实解决不了问题，因为这时整个哈希表已经退化成了一个链表，操作效率变成了 O(n)。

再来看一下扩容具体是怎么做的。由于 map 扩容需要将原有的 key/value 重新搬迁到新的内存地址，如果有大量的 key/value 需要搬迁，会非常影响性能。因此 Go map 的扩容采取了一种称为“渐进式”地方式，原有的 key 并不会一次性搬迁完毕，每次最多只会搬迁 2 个 bucket。

上面说的 hashGrow() 函数实际上并没有真正地“搬迁”，它只是分配好了新的 buckets，并将老的 buckets 挂到了 oldbuckets 字段上。真正搬迁 buckets 的动作在 growWork() 函数中，而调用 growWork() 函数的动作是在 mapassign 和 mapdelete 函数中。也就是插入或修改、删除 key 的时候，都会尝试进行搬迁 buckets 的工作。先检查 oldbuckets 是否搬迁完毕，具体来说就是检查 oldbuckets 是否为 nil。

我们先看 hashGrow() 函数所做的工作，再来看具体的搬迁 buckets 是如何进行的。

func hashGrow(t *maptype, h *hmap) {
    // B+1 相当于是原来 2 倍的空间
    bigger := uint8(1)

    // 对应条件 2
    if !overLoadFactor(int64(h.count), h.B) {
        // 进行等量的内存扩容，所以 B 不变
        bigger = 0
        h.flags |= sameSizeGrow
    }
    // 将老 buckets 挂到 buckets 上
    oldbuckets := h.buckets
    // 申请新的 buckets 空间
    newbuckets, nextOverflow := makeBucketArray(t, h.B+bigger)

    flags := h.flags &^ (iterator | oldIterator)
    if h.flags&iterator != 0 {
        flags |= oldIterator
    }
    // 提交 grow 的动作
    h.B += bigger
    h.flags = flags
    h.oldbuckets = oldbuckets
    h.buckets = newbuckets
    // 搬迁进度为 0
    h.nevacuate = 0
    // overflow buckets 数为 0
    h.noverflow = 0

    // ……
}

主要是申请到了新的 buckets 空间，把相关的标志位都进行了处理：例如标志 nevacuate 被置为 0， 表示当前搬迁进度为 0。

值得一说的是对 h.flags 的处理：

flags := h.flags &^ (iterator | oldIterator)
if h.flags&iterator != 0 {
    flags |= oldIterator
}

这里得先说下运算符：&^。这叫按位置 0运算符。例如：

x = 01010011
y = 01010100
z = x &^ y = 00000011

如果 y bit 位为 1，那么结果 z 对应 bit 位就为 0，否则 z 对应 bit 位就和 x 对应 bit 位的值相同。

所以上面那段对 flags 一顿操作的代码的意思是：先把 h.flags 中 iterator 和 oldIterator 对应位清 0，然后如果发现 iterator 位为 1，那就把它转接到 oldIterator 位，使得 oldIterator 标志位变成 1。潜台词就是：buckets 现在挂到了 oldBuckets 名下了，对应的标志位也转接过去吧。

几个标志位如下：

// 可能有迭代器使用 buckets
iterator     = 1
// 可能有迭代器使用 oldbuckets
oldIterator  = 2
// 有协程正在向 map 中写入 key
hashWriting  = 4
// 等量扩容（对应条件 2）
sameSizeGrow = 8

再来看看真正执行搬迁工作的 growWork() 函数。

func growWork(t *maptype, h *hmap, bucket uintptr) {
    // 确认搬迁老的 bucket 对应正在使用的 bucket
    evacuate(t, h, bucket&h.oldbucketmask())

    // 再搬迁一个 bucket，以加快搬迁进程
    if h.growing() {
        evacuate(t, h, h.nevacuate)
    }
}

h.growing() 函数非常简单：

func (h *hmap) growing() bool {
    return h.oldbuckets != nil
}

如果 oldbuckets 不为空，说明还没有搬迁完毕，还得继续搬。

bucket&h.oldbucketmask() 这行代码，如源码注释里说的，是为了确认搬迁的 bucket 是我们正在使用的 bucket。oldbucketmask() 函数返回扩容前的 map 的 bucketmask。

所谓的 bucketmask，作用就是将 key 计算出来的哈希值与 bucketmask 相与，得到的结果就是 key 应该落入的桶。比如 B = 5，那么 bucketmask 的低 5 位是 11111，其余位是 0，hash 值与其相与的意思是，只有 hash 值的低 5 位决策 key 到底落入哪个 bucket。

接下来，我们集中所有的精力在搬迁的关键函数 evacuate。源码贴在下面，不要紧张，我会加上大面积的注释，通过注释绝对是能看懂的。之后，我会再对搬迁过程作详细说明。

源码如下：

func evacuate(t *maptype, h *hmap, oldbucket uintptr) {
    // 定位老的 bucket 地址
    b := (*bmap)(add(h.oldbuckets, oldbucket*uintptr(t.bucketsize)))
    // 结果是 2^B，如 B = 5，结果为32
    newbit := h.noldbuckets()
    // key 的哈希函数
    alg := t.key.alg
    // 如果 b 没有被搬迁过
    if !evacuated(b) {
        var (
            // 表示bucket 移动的目标地址
            x, y   *bmap
            // 指向 x,y 中的 key/val
            xi, yi int
            // 指向 x，y 中的 key
            xk, yk unsafe.Pointer
            // 指向 x，y 中的 value
            xv, yv unsafe.Pointer
        )
        // 默认是等 size 扩容，前后 bucket 序号不变
        // 使用 x 来进行搬迁
        x = (*bmap)(add(h.buckets, oldbucket*uintptr(t.bucketsize)))
        xi = 0
        xk = add(unsafe.Pointer(x), dataOffset)
        xv = add(xk, bucketCnt*uintptr(t.keysize))、

        // 如果不是等 size 扩容，前后 bucket 序号有变
        // 使用 y 来进行搬迁
        if !h.sameSizeGrow() {
            // y 代表的 bucket 序号增加了 2^B
            y = (*bmap)(add(h.buckets, (oldbucket+newbit)*uintptr(t.bucketsize)))
            yi = 0
            yk = add(unsafe.Pointer(y), dataOffset)
            yv = add(yk, bucketCnt*uintptr(t.keysize))
        }

        // 遍历所有的 bucket，包括 overflow buckets
        // b 是老的 bucket 地址
        for ; b != nil; b = b.overflow(t) {
            k := add(unsafe.Pointer(b), dataOffset)
            v := add(k, bucketCnt*uintptr(t.keysize))

            // 遍历 bucket 中的所有 cell
            for i := 0; i < bucketCnt; i, k, v = i+1, add(k, uintptr(t.keysize)), add(v, uintptr(t.valuesize)) {
                // 当前 cell 的 top hash 值
                top := b.tophash[i]
                // 如果 cell 为空，即没有 key
                if top == empty {
                    // 那就标志它被"搬迁"过
                    b.tophash[i] = evacuatedEmpty
                    // 继续下个 cell
                    continue
                }
                // 正常不会出现这种情况
                // 未被搬迁的 cell 只可能是 empty 或是
                // 正常的 top hash（大于 minTopHash）
                if top < minTopHash {
                    throw("bad map state")
                }

                k2 := k
                // 如果 key 是指针，则解引用
                if t.indirectkey {
                    k2 = *((*unsafe.Pointer)(k2))
                }

                // 默认使用 X，等量扩容
                useX := true
                // 如果不是等量扩容
                if !h.sameSizeGrow() {
                    // 计算 hash 值，和 key 第一次写入时一样
                    hash := alg.hash(k2, uintptr(h.hash0))

                    // 如果有协程正在遍历 map
                    if h.flags&iterator != 0 {
                        // 如果出现 相同的 key 值，算出来的 hash 值不同
                        if !t.reflexivekey && !alg.equal(k2, k2) {
                            // 只有在 float 变量的 NaN() 情况下会出现
                            if top&1 != 0 {
                                // 第 B 位置 1
                                hash |= newbit
                            } else {
                                // 第 B 位置 0
                                hash &^= newbit
                            }
                            // 取高 8 位作为 top hash 值
                            top = uint8(hash >> (sys.PtrSize*8 - 8))
                            if top < minTopHash {
                                top += minTopHash
                            }
                        }
                    }

                    // 取决于新哈希值的 oldB+1 位是 0 还是 1
                    // 详细看后面的文章
                    useX = hash&newbit == 0
                }

                // 如果 key 搬到 X 部分
                if useX {
                    // 标志老的 cell 的 top hash 值，表示搬移到 X 部分
                    b.tophash[i] = evacuatedX
                    // 如果 xi 等于 8，说明要溢出了
                    if xi == bucketCnt {
                        // 新建一个 bucket
                        newx := h.newoverflow(t, x)
                        x = newx
                        // xi 从 0 开始计数
                        xi = 0
                        // xk 表示 key 要移动到的位置
                        xk = add(unsafe.Pointer(x), dataOffset)
                        // xv 表示 value 要移动到的位置
                        xv = add(xk, bucketCnt*uintptr(t.keysize))
                    }
                    // 设置 top hash 值
                    x.tophash[xi] = top
                    // key 是指针
                    if t.indirectkey {
                        // 将原 key（是指针）复制到新位置
                        *(*unsafe.Pointer)(xk) = k2 // copy pointer
                    } else {
                        // 将原 key（是值）复制到新位置
                        typedmemmove(t.key, xk, k) // copy value
                    }
                    // value 是指针，操作同 key
                    if t.indirectvalue {
                        *(*unsafe.Pointer)(xv) = *(*unsafe.Pointer)(v)
                    } else {
                        typedmemmove(t.elem, xv, v)
                    }

                    // 定位到下一个 cell
                    xi++
                    xk = add(xk, uintptr(t.keysize))
                    xv = add(xv, uintptr(t.valuesize))
                } else { // key 搬到 Y 部分，操作同 X 部分
                    // ……
                    // 省略了这部分，操作和 X 部分相同
                }
            }
        }
        // 如果没有协程在使用老的 buckets，就把老 buckets 清除掉，帮助gc
        if h.flags&oldIterator == 0 {
            b = (*bmap)(add(h.oldbuckets, oldbucket*uintptr(t.bucketsize)))
            // 只清除bucket 的 key,value 部分，保留 top hash 部分，指示搬迁状态
            if t.bucket.kind&kindNoPointers == 0 {
                memclrHasPointers(add(unsafe.Pointer(b), dataOffset), uintptr(t.bucketsize)-dataOffset)
            } else {
                memclrNoHeapPointers(add(unsafe.Pointer(b), dataOffset), uintptr(t.bucketsize)-dataOffset)
            }
        }
    }

    // 更新搬迁进度
    // 如果此次搬迁的 bucket 等于当前进度
    if oldbucket == h.nevacuate {
        // 进度加 1
        h.nevacuate = oldbucket + 1
        // Experiments suggest that 1024 is overkill by at least an order of magnitude.
        // Put it in there as a safeguard anyway, to ensure O(1) behavior.
        // 尝试往后看 1024 个 bucket
        stop := h.nevacuate + 1024
        if stop > newbit {
            stop = newbit
        }
        // 寻找没有搬迁的 bucket
        for h.nevacuate != stop && bucketEvacuated(t, h, h.nevacuate) {
            h.nevacuate++
        }

        // 现在 h.nevacuate 之前的 bucket 都被搬迁完毕

        // 所有的 buckets 搬迁完毕
        if h.nevacuate == newbit {
            // 清除老的 buckets
            h.oldbuckets = nil
            // 清除老的 overflow bucket
            // 回忆一下：[0] 表示当前 overflow bucket
            // [1] 表示 old overflow bucket
            if h.extra != nil {
                h.extra.overflow[1] = nil
            }
            // 清除正在扩容的标志位
            h.flags &^= sameSizeGrow
        }
    }
}

evacuate 函数的代码注释非常清晰，对着代码和注释是很容易看懂整个的搬迁过程的，耐心点。

搬迁的目的就是将老的 buckets 搬迁到新的 buckets。而通过前面的说明我们知道，应对条件 1，新的 buckets 数量是之前的一倍，应对条件 2，新的 buckets 数量和之前相等。

对于条件 2，从老的 buckets 搬迁到新的 buckets，由于 bucktes 数量不变，因此可以按序号来搬，比如原来在 0 号 bucktes，到新的地方后，仍然放在 0 号 buckets。

对于条件 1，就没这么简单了。要重新计算 key 的哈希，才能决定它到底落在哪个 bucket。例如，原来 B = 5，计算出 key 的哈希后，只用看它的低 5 位，就能决定它落在哪个 bucket。扩容后，B 变成了 6，因此需要多看一位，它的低 6 位决定 key 落在哪个 bucket。这称为 rehash。

map rehash

因此，某个 key 在搬迁前后 bucket 序号可能和原来相等，也可能是相比原来加上 2^B（原来的 B 值），取决于 hash 值 第 6 bit 位是 0 还是 1。

再明确一个问题：如果扩容后，B 增加了 1，意味着 buckets 总数是原来的 2 倍，原来 1 号的桶“裂变”到两个桶。

例如，原始 B = 2，1号 bucket 中有 2 个 key 的哈希值低 3 位分别为：010，110。由于原来 B = 2，所以低 2 位 10 决定它们落在 2 号桶，现在 B 变成 3，所以 010、110 分别落入 2、6 号桶。

bucket split

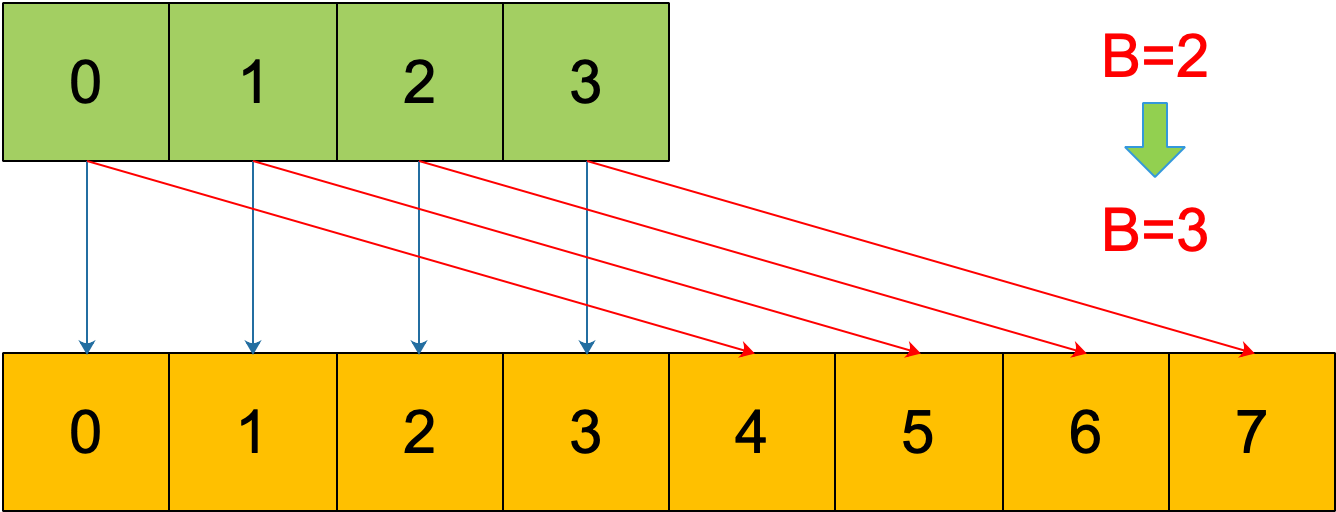
理解了这个，后面讲 map 迭代的时候会用到。

再来讲搬迁函数中的几个关键点：

evacuate 函数每次只完成一个 bucket 的搬迁工作，因此要遍历完此 bucket 的所有的 cell，将有值的 cell copy 到新的地方。bucket 还会链接 overflow bucket，它们同样需要搬迁。因此会有 2 层循环，外层遍历 bucket 和 overflow bucket，内层遍历 bucket 的所有 cell。这样的循环在 map 的源码里到处都是，要理解透了。

源码里提到 X, Y part，其实就是我们说的如果是扩容到原来的 2 倍，桶的数量是原来的 2 倍，前一半桶被称为 X part，后一半桶被称为 Y part。一个 bucket 中的 key 可能会分裂落到 2 个桶，一个位于 X part，一个位于 Y part。所以在搬迁一个 cell 之前，需要知道这个 cell 中的 key 是落到哪个 Part。很简单，重新计算 cell 中 key 的 hash，并向前“多看”一位，决定落入哪个 Part，这个前面也说得很详细了。

有一个特殊情况是：有一种 key，每次对它计算 hash，得到的结果都不一样。这个 key 就是 math.NaN() 的结果，它的含义是 not a number，类型是 float64。当它作为 map 的 key，在搬迁的时候，会遇到一个问题：再次计算它的哈希值和它当初插入 map 时的计算出来的哈希值不一样！

你可能想到了，这样带来的一个后果是，这个 key 是永远不会被 Get 操作获取的！当我使用 m[math.NaN()] 语句的时候，是查不出来结果的。这个 key 只有在遍历整个 map 的时候，才有机会现身。所以，可以向一个 map 插入任意数量的 math.NaN() 作为 key。

当搬迁碰到 math.NaN() 的 key 时，只通过 tophash 的最低位决定分配到 X part 还是 Y part（如果扩容后是原来 buckets 数量的 2 倍）。如果 tophash 的最低位是 0 ，分配到 X part；如果是 1 ，则分配到 Y part。

这是通过 tophash 值与新算出来的哈希值进行运算得到的：

if top&1 != 0 {
    // top hash 最低位为 1
    // 新算出来的 hash 值的 B 位置 1
    hash |= newbit
} else {
    // 新算出来的 hash 值的 B 位置 0
    hash &^= newbit
}

// hash 值的 B 位为 0，则搬迁到 x part
// 当 B = 5时，newbit = 32，二进制低 6 位为 10 0000
useX = hash&newbit == 0

其实这样的 key 我随便搬迁到哪个 bucket 都行，当然，还是要搬迁到上面裂变那张图中的两个 bucket 中去。但这样做是有好处的，在后面讲 map 迭代的时候会再详细解释，暂时知道是这样分配的就行。

确定了要搬迁到的目标 bucket 后，搬迁操作就比较好进行了。将源 key/value 值 copy 到目的地相应的位置。

设置 key 在原始 buckets 的 tophash 为 evacuatedX 或是 evacuatedY，表示已经搬迁到了新 map 的 x part 或是 y part。新 map 的 tophash 则正常取 key 哈希值的高 8 位。

下面通过图来宏观地看一下扩容前后的变化。

扩容前，B = 2，共有 4 个 buckets，lowbits 表示 hash 值的低位。假设我们不关注其他 buckets 情况，专注在 2 号 bucket。并且假设 overflow 太多，触发了等量扩容（对应于前面的条件 2）。

扩容前

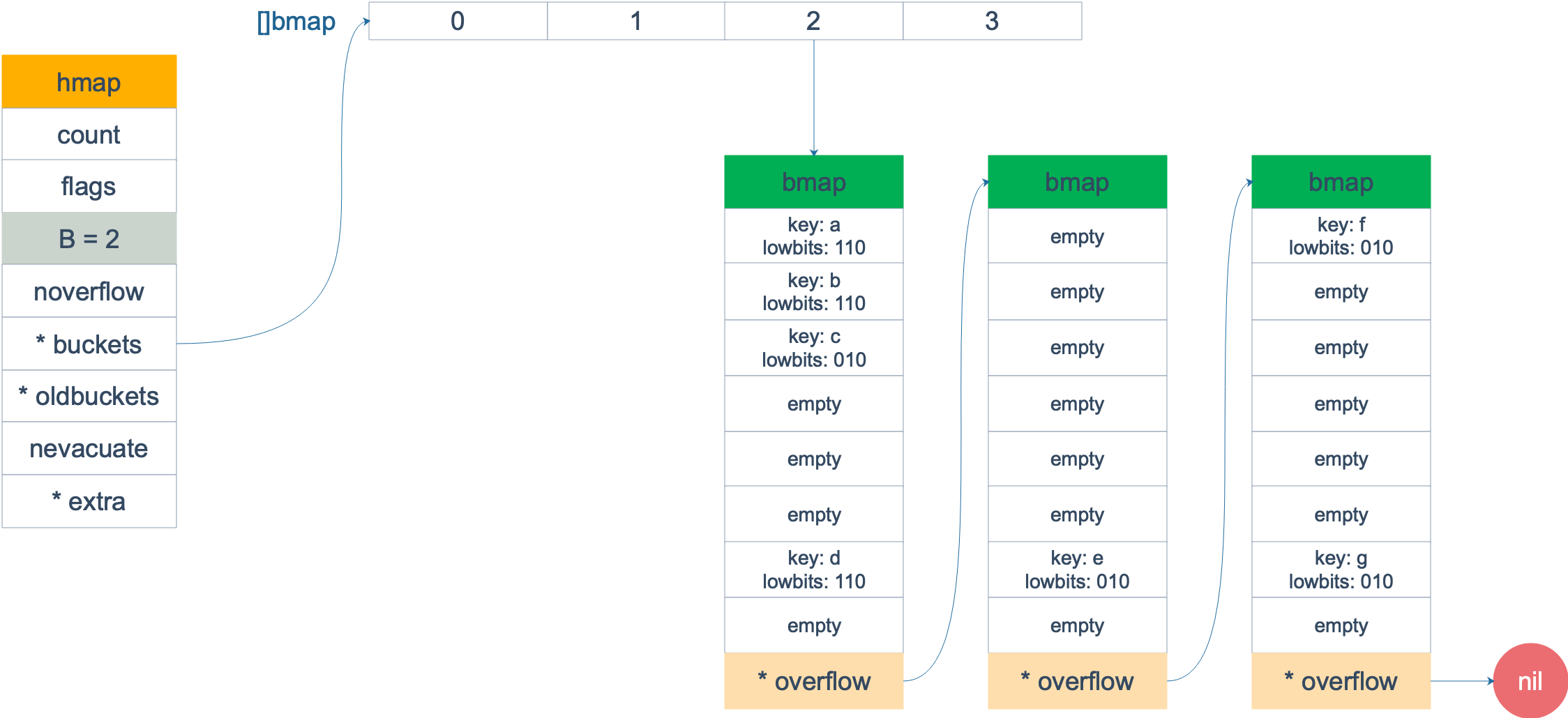
扩容完成后，overflow bucket 消失了，key 都集中到了一个 bucket，更为紧凑了，提高了查找的效率。

same size 扩容

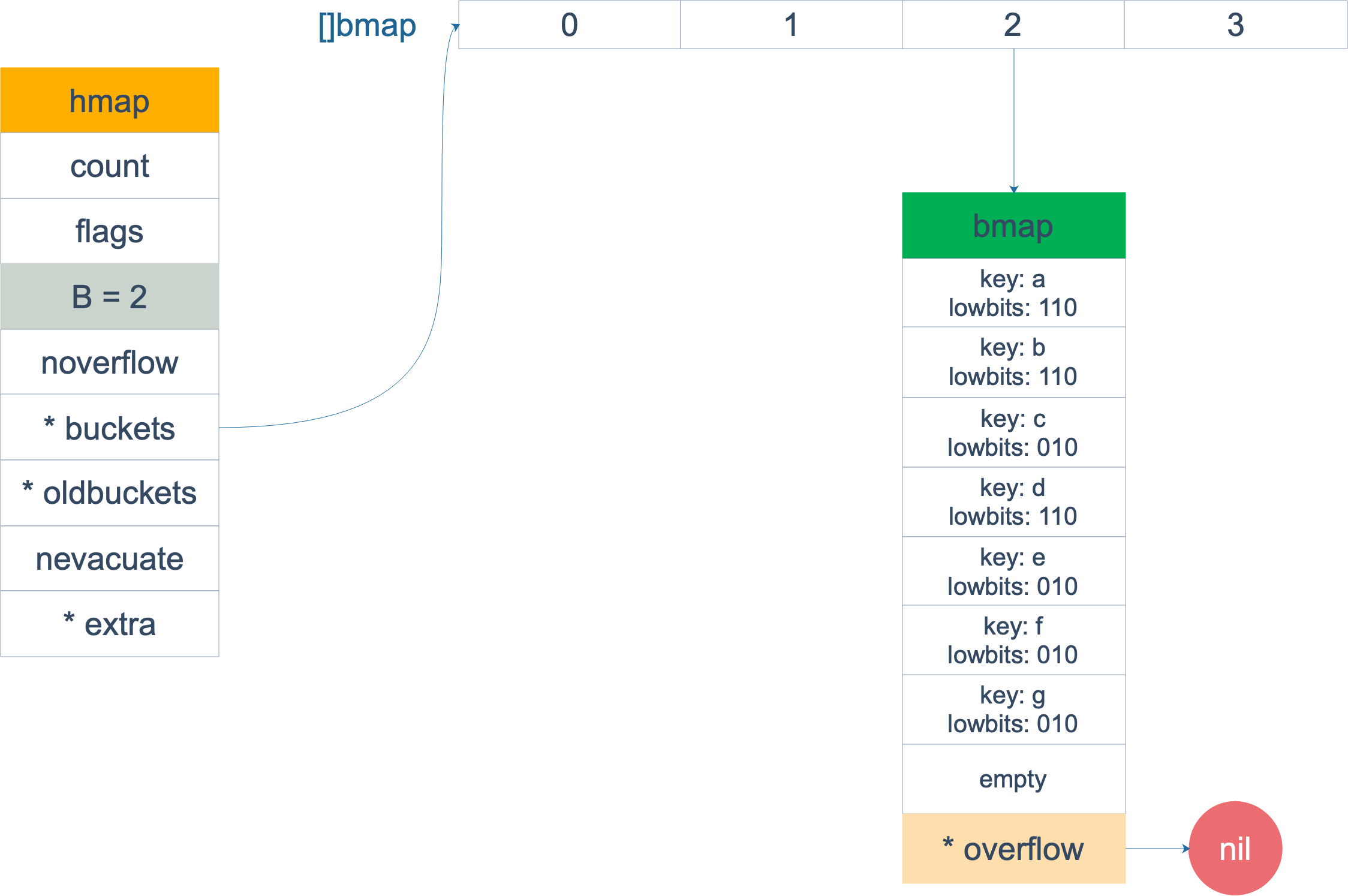
假设触发了 2 倍的扩容，那么扩容完成后，老 buckets 中的 key 分裂到了 2 个 新的 bucket。一个在 x part，一个在 y 的 part。依据是 hash 的 lowbits。新 map 中 0-3 称为 x part，4-7 称为 y part。

2倍扩容

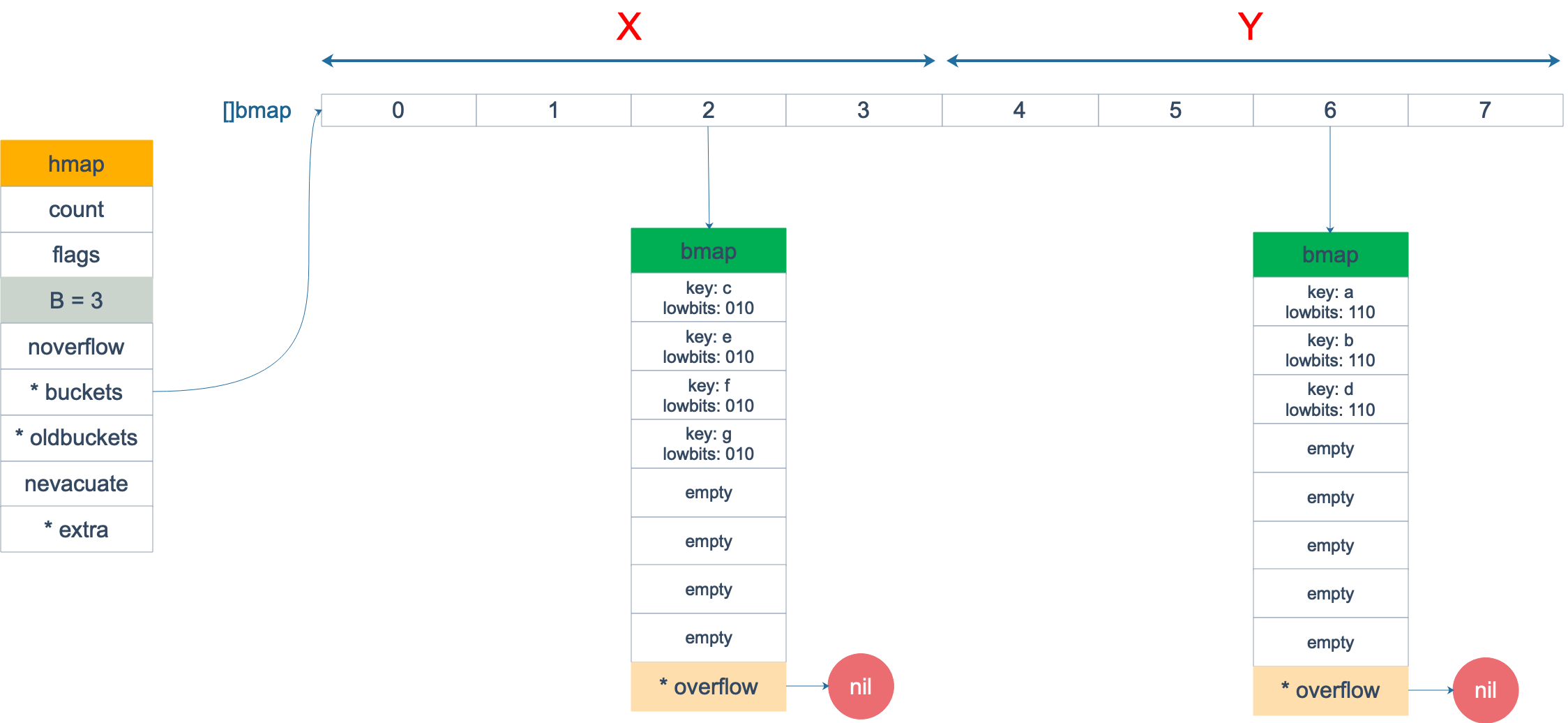
注意，上面的两张图忽略了其他 buckets 的搬迁情况，表示所有的 bucket 都搬迁完毕后的情形。实际上，我们知道，搬迁是一个“渐进”的过程，并不会一下子就全部搬迁完毕。所以在搬迁过程中，oldbuckets 指针还会指向原来老的 []bmap，并且已经搬迁完毕的 key 的 tophash 值会是一个状态值，表示 key 的搬迁去向。